Bevezetés, irodalmi áttekintés
A cikkben az írások alapegységeit grafémáknak nevezzük, amelyeknek különböző tulajdonságai vannak: van alakjuk, amit gyakran betűalaknak hívunk, van hangértékük, valamint van használati idejük. Betűalakból és hangértékből több is lehet. A grafémaalakok közül a legszabályosabbat kiemelten szoktunk kezelni, ezt normalizált grafémaalaknak nevezzük, és rendszerint ezzel hivatkozunk az adott grafémára. Egy adott felhasználói környezetben ideálisnak tekintett, de a normalizálttól esetleg eltérő grafémaalakot tipizáltnak nevezzük. A grafémának a feliratokban megjelenő megvalósulásai a graféma valamelyik tipizált alakját közelítik.
A kifejlesztett jelentésazonosító módszert a 15–17. századi székely-magyar rovással írt, egyes esetekben grafémahiányos, grafémahibás írások megfejtéséhez alkalmaztuk. Az általunk végzett írásazonosítás eltér az optikai karakterfelismerés (OCR) jól ismert feladatától. Amíg ugyanis az OCR esetében az írás grafémáinak normalizált alakját és tipizált alakjait ismertnek tételezhetjük fel, és egy feliratban található képi információt kell megfeleltetni valamelyik ismert grafémának, addig az írásazonosítás során a feliratban található képi információt úgy kell valamilyen grafémához rendelni, hogy a graféma tipizált betűalakja gyakran ismeretlen. Az általunk elvégzett vizsgálatok során a feliratokban lévő egy jelek képi információit emberi beavatkozással célszerűen választott topológiai tulajdonságvektorok értékeinek megadásával leírtuk, és az egyes jelekre kapott tulajdonságvektorok-értékeket mint kiindulási adatot alkalmaztuk az írásazonosítási eljárás bemeneti adatsoraként (Tóth és tsai. 2012).
Az előbbiek szerint a felirat egyes jeleire meghatározott topológiai tulajdonságvektorok alapján algoritmusunk a felirat egyes jeleit hozzárendeli az ismert grafémák valamelyikéhez. A hozzárendelés pontosságát úgy minősíti, hogy összehasonlítja a felirat jeleire kapott tulajdonságvektorokat az ismert grafémák grafémaalakjaihoz tartozó tulajdonságvektorokkal. Ezután egy beépített szótár segítségével, illetve a szövegkörnyezet figyelembevételével próbálja meghatározni a felismerésre beadott szó létezését és az azonosításnak a statisztikus hibabecslésen alapuló relevanciáját. Így az algoritmus kimeneteként egy vagy több szót várhatunk különböző valószínűségi értékekkel, amelyekből a felirat történelmi, régészeti jellemzői alapján kiválasztható a legvalószínűbb értelmezés.
A korábbi időkben készített írások olvasása, értelmezése számos nehézséget okoz a kutatók számára. Ennek oka az írást hordozó anyag (fa, kő, tégla, papír stb.) romlásától eltekintve elsősorban az, hogy az írásokban használatos betűk alakjai idővel változtak, továbbá a különböző írásemlékeket eltérő kézírással és ismeretekkel rendelkező emberek hozták létre. A nemzetközi szakirodalomban széles körű kutatást folytattak ezen a területen (Doermann & Jaeger 2006). Többek között értékes eredményeket értek el az Indiában kannada nyelvet beszélők között az 5. század óta használatos helyi kannada írás emlékei korának algoritmikus meghatározásában. A cikkben közölt eljárás neurális hálózatok alkalmazásával kísérli meg a különböző történelmi korokban használatos betűalakokra (glyph) jellemző azonosítók felismerését egy tetszőleges szövegben. A kannada íráshoz tartozó számjegyek felismerésére többszintű osztályozókat alkalmaztak, amelyeket fuzzy logika (az elmosódott halmazok logikája, ahol figyelembe veszik, hogy az egymást kizáró állítások között lehet átmeneti tartomány is) segítségével összegeztek (Harish Kashyap és tsai. 2003). Az egyiptomi hieroglif írás megfejtésére is többen dolgoztak ki jelentésazonosító algoritmusokat, például Jón és társai, akik képfeldolgozás után neurális hálózat segítségével azonosítottak egyiptomi hieroglifákat (Jón 2009). Sikereket értek el Le Cun és társai a kézzel írott latin számjegyek azonosításában (Le Cun és tsai. 2004). Hasonlóan ígéretes eredményeket ért el egy másik kutatócsoport a régi perzsa írások felismerési eljárásának kidolgozásában (Izadi és tsai. 2008).
A székely-magyar rovás a rovás íráscsaládba tartozik és a Nagyszentmiklósi kincsen is megtalálható Kárpát-medencei rovásból származik (Hosszú 2013). Eredete az utóbbi évtizedekben tisztázódott. A rovásírások családja döntő részben ugyanabból a föníciai írásból ered, ahonnan többek között a görög és a latin betűs írás is. A rovás egy sajátos ágát, a székely-magyar rovást a székelyek őrizték meg és használták évszázadokon át. A rovásírás hangjelölése alfabetikus elveken alapul: minden hanghoz egy betűt rendel. Az írásirány a legtöbb esetben jobbról balra halad, de szórványosan felbukkannak balról jobbra haladó emlékek is. Az utóbbi esetben az írásjegyek függőlegesen tükrözendők. A kis- és nagybetűk között különbségtétel nincs, noha néha a tulajdonnevek kezdőbetűjét egyes emlékeken kicsit nagyobbnak írták. Megjegyzendő, hogy ez az ómagyar kori latin betűs szövegekben is így van. A székely-magyar rovás feliratok fába és kőbe karcolva, ill. a 15. századtól kezdve papírra írva maradtak fenn (Hosszú 2012).
Jelen cikkben olyan hazai kutatás első eredményeiről számolunk be, amely részben nem ismert grafémaalakokat használó rovásírással (Hosszú 2012), évszázadokkal ezelőtt készített feliratok jelentésazonosításához kíván a kutatóknak segítséget nyújtani matematikai statisztikai eszközök segítségével. A kidolgozott eljárás az egyes grafémák topológiai felbontására (Pardede és tsai. 2012), a vizsgált feliraton azonosítható stílusjegyekre és azok kiértékelésére kifejlesztett algoritmusra épül, továbbá felhasználja az eddig ismert székely-magyar rovásábécék betűalak-tárát, illetve egy beépített, bővíthető magyar szótárat, amelyben a szavakat hangalakjuk formájában tároljuk.
A kifejlesztett eljárás
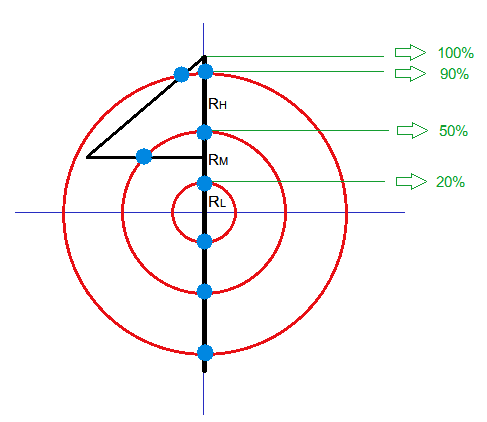
Az általunk kifejlesztett, a rovásfeliratokra optimalizált jelentésazonosító eljárás algoritmizálhatóságának fő akadálya az volt, hogy a feliratokon az egyes grafémaalakok gyakran néhány fokos szögben elfordulva jelennek meg, így azok felismerése és a szükséges grafémaalakot leíró topológiai tulajdonságvektor meghatározása erősen szubjektív döntést igényelhet. Ennek a nehézségnek az áthidalására kifejlesztettünk egy jelentésazonosítási módszert, amivel figyelmen kívül hagyhatjuk a grafémákat felépítő topológiai szerkezeti egységek elfordulási szögét, és amelyhez Heutte és társai (1998) módszerének egy általunk továbbfejlesztett változatát alkalmazzuk. Ezzel olyan eljárást nyertünk, amely a korábbiaknál kevésbé érzékeny a grafémák topológiai szerkezetének hibáira. Az általunk javasolt fejlesztés lényege, hogy a Heutte és társai által alkalmazott négyzetrács helyett köröket illesztünk a grafémákra (1. ábra). A körvonalak és a graféma vonalának metszéspontjai adják meg az új tulajdonság-vektorunkat; vagyis összeszámoljuk, hogy a kis körnek (RL), a középső körnek (RM) és a nagy körnek (RH) hány metszéspontja van a grafémával. A metszéspontokat kis, kitöltött körökkel szemléltetjük.
1. ábra: A rovás ![]() A grafémája (fekete vonal) köré szerkesztett körök sugarainak és középpontjának meghatározása.
A grafémája (fekete vonal) köré szerkesztett körök sugarainak és középpontjának meghatározása.
A körök középpontjának meghatározásához több kritériumot is létrehoztunk, amelyek közül azt választjuk, ami az éppen vizsgált graféma topológiájához jobban illeszkedik:
- ha a vizsgált grafémának csak egy egyenes fő vonala van, akkor annak mértani közepe lásd 1. ábra;
- ha a vizsgált grafémának csak egy fő vonala van és az egy körív, megszerkesztjük az ív húrját, és annak mértani közepe;
- ha a vizsgált grafémának több fő vonala van, a grafémát határoló téglalap középpontját definiáljuk a körök középpontjának, mint a Khan által is használt „boundary box”, azaz a „határoló téglalap” módszerrel (Khan 2000).
Kezdeti vizsgálataink azt mutatják, hogy két kör nem elégséges a grafémák megkülönböztetéséhez, de három olyan kör már igen, amelyek a sugarai a következők: RHigh (RH) = 90%*HG/2, RMedium (RM) = 50%*HG/2, RLow (RL) = 20%*HG/2. Az RHigh ≤ HG vagyRHigh ≤ WG feltételeknek teljesülniük kell, ahol R a körök sugarát, HG a graféma magasságát, és WG a graféma szélességét jelöli.
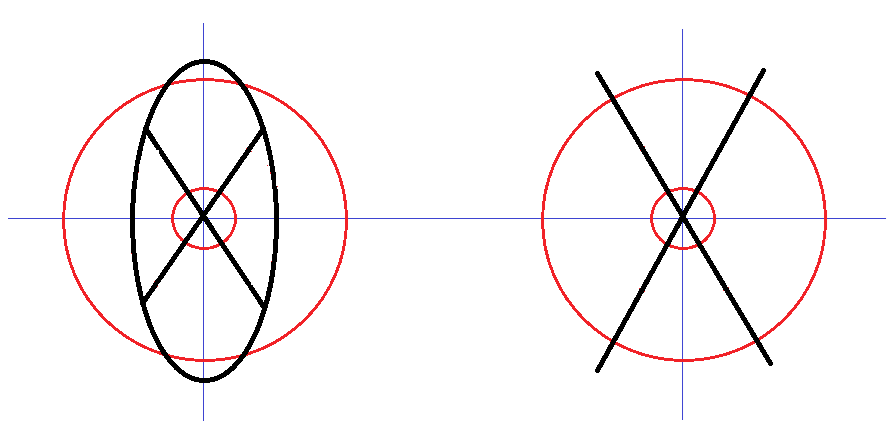
A 2. ábra két kör alkalmazására mutat példát. Az a) ábra a rovás ![]() F, a b) ábra a rovás
F, a b) ábra a rovás ![]() B grafémákra szerkesztett körök és a grafémák vonalainak metszéspontjából számolt (RL,RH) vektor értéke, amely mindkét esetben (4,4), pedig a két graféma különbözik egymástól. Hasonló eredményre jutottunk több másik graféma vizsgálatánál is.
B grafémákra szerkesztett körök és a grafémák vonalainak metszéspontjából számolt (RL,RH) vektor értéke, amely mindkét esetben (4,4), pedig a két graféma különbözik egymástól. Hasonló eredményre jutottunk több másik graféma vizsgálatánál is.
2. ábra: A körök számának a meghatározása a 2 körös esetben:
bal oldal: ![]() F graféma (RL,RH) = (4,4), jobb oldal:
F graféma (RL,RH) = (4,4), jobb oldal: ![]() B graféma (RL,RH) = (4,4).
B graféma (RL,RH) = (4,4).
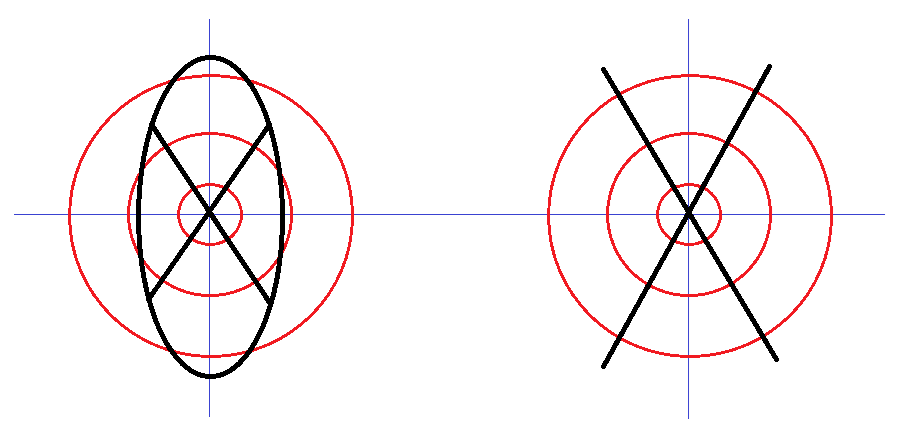
A módszert megismételtük három kör alkalmazásával, amelyre a 3. ábra mutatja a példát. A c) ábrán az ![]() F graféma (RL,RM,RH) vektorának értéke(4,8,4), míg a d) ábrán a
F graféma (RL,RM,RH) vektorának értéke(4,8,4), míg a d) ábrán a ![]() B graféma (RL,RM,RH) vektorának értéke(4,4,4)-et adott. Az ismert székely-magyar rovás grafémák elemzése azt mutatta, hogy három kör szükséges ahhoz, hogy a székely-magyar rovás grafémákat meg tudjuk különböztetni egymástól.
B graféma (RL,RM,RH) vektorának értéke(4,4,4)-et adott. Az ismert székely-magyar rovás grafémák elemzése azt mutatta, hogy három kör szükséges ahhoz, hogy a székely-magyar rovás grafémákat meg tudjuk különböztetni egymástól.
3. ábra: Körök számának a meghatározása a 3 körös esetben:
bal oldal: ![]() F graféma (RL,RM,RH) = (4,8,4), jobb oldal:
F graféma (RL,RM,RH) = (4,8,4), jobb oldal: ![]() B graféma (RL,RM,RH) = (4,4,4).
B graféma (RL,RM,RH) = (4,4,4).
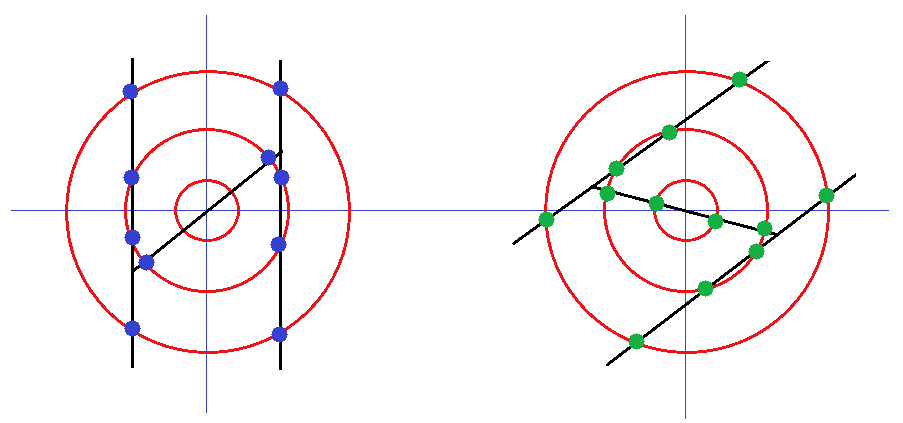
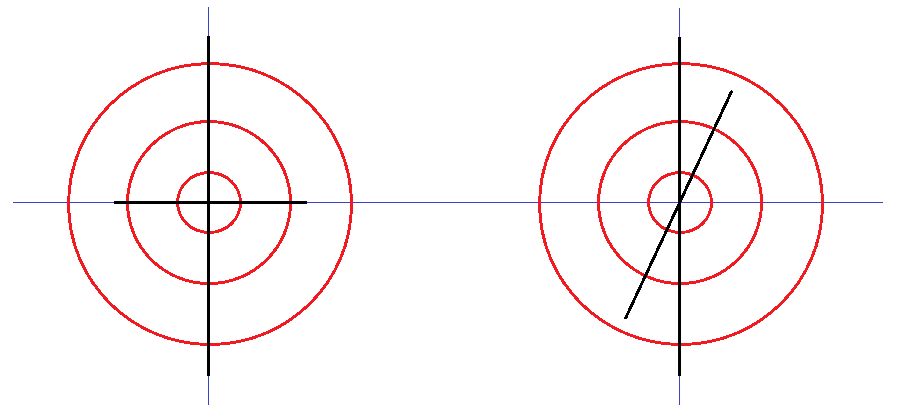
A következőkben megvizsgáljuk, hogy az általunk fejlesztett körmódszerrel milyen eredményeket szolgáltat a normalizált és egy nem normalizált székely-magyar rovás R grafémáinak az elemzése. A 4. ábra c) esetében az (RL,RM,RH) vektor értéke (0,6,4), míg d) esetben a (RL,RM,RH) vektor értéke szintén (0,6,4)-et ad eredményül. Láthatjuk, hogy ugyanazon székely-magyar rovás grafémára normalizált, illetve nem normalizált esetben is ugyanazt az eredményt kaptuk, ami a módszerünk előnye.
4. ábra: A rovás ![]() R grafémára szerkesztett körök és a graféma vonalának metszéspontja, bal oldal: normalizált graféma, jobb oldal: középpontja körül elforgatott graféma.
R grafémára szerkesztett körök és a graféma vonalának metszéspontja, bal oldal: normalizált graféma, jobb oldal: középpontja körül elforgatott graféma.
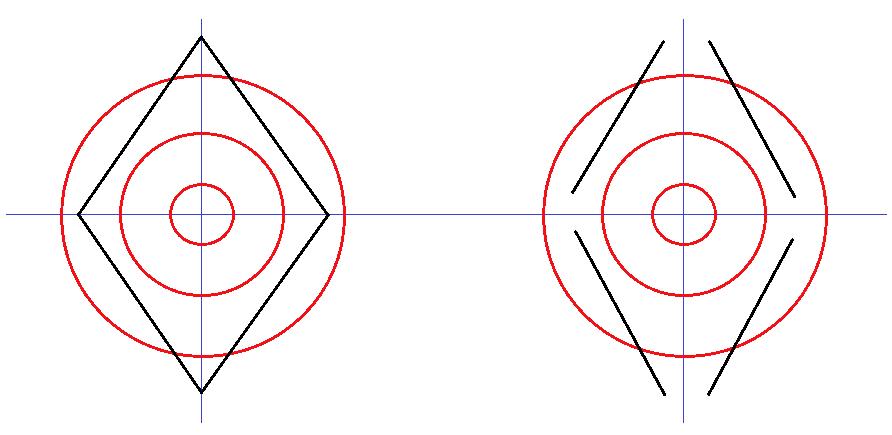
A módszer alkalmazására mutatunk be további példákat normalizált és topológiai szerkezetükben sérült székely-magyar rovás grafémákon. Amint az az 5. ábrán és a 6. ábrán látható, módszerünk a normalizált grafémákra, illetve azok egyik lehetséges topológiai szerkezetben eltérő variánsaira is ugyanazt a vektorértéket adja.
5. ábra: A rovás ![]() D graféma és variánsa: (RL,RM,RH) = (4,4,2)
D graféma és variánsa: (RL,RM,RH) = (4,4,2)
6. ábra: A rovás ![]() K graféma és variánsa: (RL,RM,RH) = (0,0,4)
K graféma és variánsa: (RL,RM,RH) = (0,0,4)
Eredmények
Az alábbiakban összehasonlítjuk a székely-magyar rovásra kidolgozott jelentésazonosító algoritmusunk működését az általunk kifejlesztett körmódszer nélkül, illetve a körmódszer alkalmazásával. Egy vizsgálati célból létrehozott rovásfeliratot adtunk az algoritmusunkra írt alkalmazás bemenetére. Ismeretlen grafémaként definiáltuk a ![]() jelet, míg az
jelet, míg az ![]() N,
N, ![]() T és
T és ![]() L ismert székely-magyar rovás grafémák. Az algoritmus bemenete (megfejtendő felirat balról jobbra írásiránnyal olvasva):
L ismert székely-magyar rovás grafémák. Az algoritmus bemenete (megfejtendő felirat balról jobbra írásiránnyal olvasva): ![]() . Az algoritmus ezek után megkeresi az ismeretlen felirat minden egyes jeléhez, azok topológiai tulajdonságai alapján, a hozzá legközelebb álló ismert székely-magyar rovás grafémákat. A grafémákhoz tartozó grafémanevekkel egyszerűsítést végez, majd jelsorozatokat képez belőlük. Végül a jelsorozatokba visszahelyettesíti az adott grafémanévhez tartozó hangalakokat. Ezután az algoritmus a hangalakjuk formájában tárolt magyar szavak szótárából kiválasztja a kapott hangsorozatoknak megfelelő szavakat.
. Az algoritmus ezek után megkeresi az ismeretlen felirat minden egyes jeléhez, azok topológiai tulajdonságai alapján, a hozzá legközelebb álló ismert székely-magyar rovás grafémákat. A grafémákhoz tartozó grafémanevekkel egyszerűsítést végez, majd jelsorozatokat képez belőlük. Végül a jelsorozatokba visszahelyettesíti az adott grafémanévhez tartozó hangalakokat. Ezután az algoritmus a hangalakjuk formájában tárolt magyar szavak szótárából kiválasztja a kapott hangsorozatoknak megfelelő szavakat.
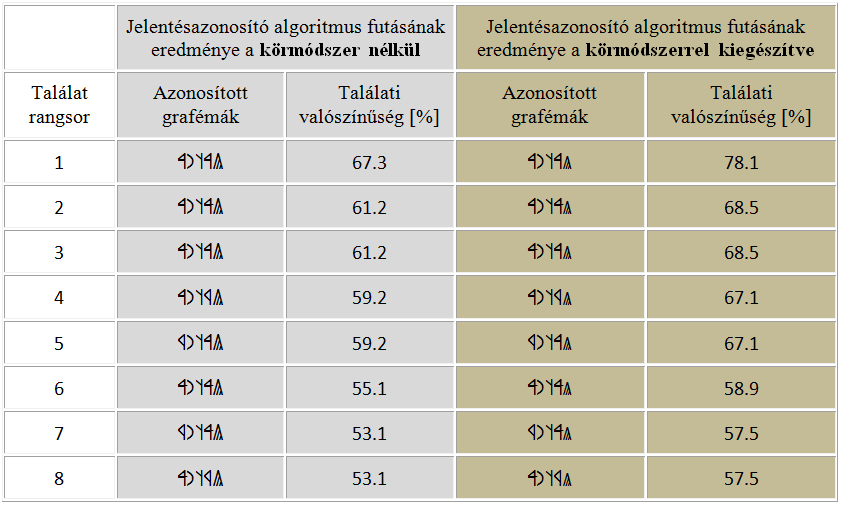
A szótárban talált szavakból az algoritmus rovásgrafémákkal leírt szavakat képez, és az egyes grafémákhoz tartozó topológiai tulajdonságvektorokból kiszámolja a megfejteni kívánt szó és a székely-magyar rovásgrafémákkal felírt szavak közti hasonlóságot és ez alapján rangsorolja a találatokat. A körmódszerrel kiegészített algoritmust megvalósítottuk egy szoftverben, amelynek eredményét az 1. táblázat mutatja be.
1. táblázat: A körmódszer nélkül és a körmódszer alkalmazásával kapott eredmények.
Az 1. táblázatból látható, hogy a körmódszer bevezetésével jelentősen javult a jelentésazonosító algoritmusunk megfejtési hatékonysága.
Összefoglalás, következtetések
A székely-magyar rovásra kidolgozott jelentésazonosító algoritmusunkat továbbfejlesztettük a grafémák köré szerkesztett koncentrikus körök módszerével. A tesztfuttatások azt igazolják, hogy a körmódszerrel felvértezett alkalmazás elő-feldolgozó algoritmusa a nehezen olvasható grafémához relevánsabb prioritás sorrendet állít fel az ismert grafémákból, mint a körmódszer alkalmazása nélkül. Egy ismeretlen szimbólumsorozat megfejtésének valószínűségi becslésére pontosabb eredményeket szolgáltat, mivel e módszerrel lényegében a grafémák hasonlósági faktora robusztusabb lett.
A cikkben bemutattuk a grafémák és négyzetrácsok metszetének vizsgálata során felmerülő nehézséget, rávilágítottunk, illetve bebizonyítottuk, hogy az általunk fejlesztett körmódszer miért hatásosabb a négyzetrácsok módszeréhez képest, és miért használható normalizálás előtti grafémák vizsgálatára.
Jelen cikkben közölt új módszerünk önállóan nem alkalmas a székely-magyar rovás grafémák tökéletes megkülönböztetéséhez, illetve azonosításához. A cikkben példákkal illusztráltuk az egyes grafémákon és azok variánsain, hogy míg a graféma topológia szerkezetének sérülése a topológiai tulajdonságvektor összetételét jelentősen befolyásolja, addig a körmódszer kevésbé érzékeny erre. A korábban publikált (Tóth és tsai. 2010) tulajdonságvektoros módszerünkkel együtt alkalmazva a körmódszert, jelentős mértékben javult a nehezen olvasható, stílusukban különböző székely-magyar rovás feliratok megfejtésére kidolgozott algoritmusunk találati becslése.
Irodalomjegyzék
Doermann, David – Jaeger, Stefan (2006): Arabic and Chinese Handwriting Recognition, Berlin, Heidelberg: Springer, SACH 2006 Summit College Park, MD, USA, September 27-28, 2006.
Harish Kashyap, Krishnamurthy – Bansilal – Arun Koushik, Parthasarathy (2003): Hybrid neural network architecture for age identification of ancient Kannada scripts. Proceedings of the 2003 IEEE International Symposium on Circuits and Systems (ISCAS) 5(25-28) May 2003, pp. V-661 – V-664.
Heutte, Laurent – Paquet, Thierry – Moreau, J.V. – Lecourtier, Yves – Olivier, C. (1998): A structural/statistical feature based vector for handwritten character recognition. Pattern Recognition Letters 19: 629-641. Elsevier.
Hosszú Gábor (2010): Az informatika írástörténeti alkalmazásai. In IKT 2010, Informatika Korszerű Technikái Konferencia, meghívott plenáris előadás, 2010. március 5-6., Dunaújvárosi Főiskola, Dunaújváros. Szerk.: Dr. Cserny László. ISBN 978-963-9915-38-1, 5-21. o.
Hosszú, Gábor (2012): Heritage of Scribes. The Relation of Rovas Scripts to Eurasian Writing Systems. Budapest: Rovás Foundation. Második, bővített kiadás.
Hosszú Gábor (2013): Rovásatlasz. Budapest: Milani Kft., ISBN 978-963-08-5812-0.
Izadi, Sara – Sadri, Javad – Solimanpour, Farshid – Suen, Ching Y. (2008): A review on Persian script and recognition techniques. In Arabic and Chinese Handwriting Recognition. Lecture Notes in Computer Science. Springer Berlin, Heidelberg, March 13, 2008.
Jón Orri Kristjánsson (2009): Glyph identification using neural network techniques. HORUS project. http://skemman.is//handle/1946/1015, letöltve 2013. május 20-án.
Khan, N.A. (2000): Thesis: A Shape Analysis Model with Application to Character and Word Recognition. Eindhoven: Technische Universiteit Eindhoven, 2000, Proefschrift. ISBN 90-386-1750-X.
Le Cun, Yann – Boser, Bernhard – Denker, John S. (2013): Handwritten Digit Recognition with a Back-Propagation Network, http://yann.lecun.com/exdb/publis/pdf/lecun-90c.pdf, letöltve 2013. május 20.-án.
Pardede, Raymond E. I. – Tóth, Loránd Lehel – Hosszú, Gábor – Kovács, Ferenc (2012): Pattern Identification for Computerized Paleography. In Scientific Workshop organized by the PhD school on Computer Science in the framework of the project TÁMOP-4.2.2/B-10/1-2010-0009. 2012., megjelenés alatt.
Tóth Loránd – Hosszú Gábor – Dian Szabolcs – Pardede, Raymond – Kovács Ferenc (2010): Jelentésazonosító eljárás a 16-18. századi székely-magyar rovásemlékek értelmezésére. In IKT2010, Informatika Korszerű Technikái Konferencia, 2010. március 5-6., Dunaújvárosi Főiskola, Dunaújváros. Kiadó: Szerk.: Dr. Cserny László. ISBN 978-963-9915-38-1. 5-21. o.
Tóth Loránd – Hosszú Gábor – Pardede, Raymond (2012): Grafémák kanonikus összetevőkre bontása. In ASZPK2012, I. Alkalmazott Számítógépes Paleográfiai Konferencia, 2012. december 1., Budapesti Műszaki és Gazdaságtudományi Egyetem, Budapest. Szerk.: Dr. Hosszú Gábor. megjelenés alatt.
Nincs hozzászólás!