A továbbiakban egy konkrét eset leírása következik, melynek során matematikai eszközökkel vizsgáltak, és jutottak közelebb egy filológiai kérdés megválaszolásához.
A kérdés így szólt: Kinek tulajdonítható a Nachtwachen. Von Bonaventura (továbbiakban Nachtwachen) című 1804-es keletkezésű német regény. Az irodalomtörténészek számára nyilvánvaló volt, hogy a Bonaventura egy írói álnév, de közel kétszáz éven keresztül nem tudták megállapítani, hogy ki lehet a tényleges szerző. A megoldáshoz végül egy német fizikus-matematikus, Dieter Wickmann módszere, és további statisztikai vizsgálatok vezettek. Az ő 1969-ben megjelent doktori disszertációja (Wickmann 1969) ennek a leírásnak a fő forrása.
Wickmann azt írja disszertációjának bevezetőjében, hogy „Liest ein Kundiger einen ihm bisher unbekannten Text eines Verfassers, der zu einer ihm bekannten Gruppe von Verfassern gehört, so wird er im allgemeinen den Text dem richtigen Verfasser zuordnen können.” (Ha egy hozzáértő személy egy eddig ismeretlen szerzőjű szöveget olvas, aki egy meghatározott szerzői csoportba tartozik, akkor általában képes a szöveget a megfelelő szerzőnek tulajdonítani, WICKMANN 1969.) Ezzel arra utal, hogy az egyes szerzők stílusát tanulmányozva és jól megismerve a szövegek stílusából következtethetünk kellő szakértelemmel a szöveg szerzőjére. Ezzel próbálkoztak is a filológusok, több-kevesebb sikerrel. A tanulmány megszületéséig a Nachtwachen stílusát tanulmányozó szakértők négy lehetséges szerzőre szűkítették a kutatást, akik a szöveg keletkezésének korában alkottak hasonló stílusban. A négy szerző Clemens Brentano, E.T.A. Hoffmann, Karl Friedrich Gottlob Wetzel és Caroline Schelling. Ezen szerzők részletesebb vizsgálatával igyekezett a Bayes-statisztikus megállapítani, hogy ki a tényleges szerző.
A kutatást nem minden alapot nélkülözve kezdte, ugyanis a szintén az Aacheni Egyetemen dolgozó munkatársa, Josef Lauter egy korábbi, 1966-os disszertációjában (Lauter 1966) hasonló kérdéseket vizsgált: bizonyos grammatikai elemek, úgynevezett Wortartdigrammen (’szótípuspárok’) relatív gyakoriságát vizsgálta három szerző, Kant, Goethe és Herder szövegeiben, 10.000, illetve 20.000 elemű mintákban. A Lauter-tanulmány pusztán elméleti alapokon foglalkozott irodalmi szövegek statisztikai vizsgálatával, de fontos megállapítást tett. „Deutlich sind die Schwankungen innerhalb der Autoren geringer als die zwischen ihnen.” (Egyértelműen kisebb az ingadozás a szerzőkön belül, mint egymás között, WICKMANN 1969.) Erre vonatkozik az 1-es ábra.

A diagrammon a vízszintes tengelyen a különböző szótípuspárok találhatók, úgymint melléknév-főnév, befejezett igealak-névmás, befejezetlen igealak-segédige, valamint pont-befejezett igealak. Ezt úgy kell érteni, hogy azon esetek számát vizsgáljuk, amikor a szövegekben például melléknevet közvetlenül főnév követ stb. Értelemszerűen K=Kant, G=Goethe, H=Herder. A függőleges tengelyen a relatív gyakoriságok láthatók százalékos alakban. Ezek alapján a vizsgálat szerint az egyes szótípuspárok relatív gyakorisága a 20.000 elemű mintákban (ezek a tömör oszlopok) nem sokban tér el a 10.000 elemű mintához képest (a szaggatott szélű oszlopok) az egyes szerzőkön belül. Ezzel szemben feltűnő a különbség a szerzők között. Ez a vizsgálat természetesen nem vezet hosszabb távú következtetésekhez, de megfelelő alapot nyújt további, részletesebb vizsgálatokhoz.
Így jutunk el a Wickmann-féle módszerhez, melynek lényege a következőben foglalható össze: „Die eventuelle Lösung der Aufgabe impliziert die Hoffnung, verschieden Autoren schreiben mit verschiedenen und je spezifischen Parametern, deren Differenz genügend groß ist, in einer Stichprobe von relativ geringem Umfang entdeckt zu werden.” (A feladat végső megoldása megában foglalja a reményt, hogy különböző szerzők különböző és nagyon specifikus paraméterekkel írnak, melyek között elegendően nagy a különbség, hogy egy megfelelően nagy mintából felismerhetőek legyenek, WICKMANN 1969.) Ezen elv mentén dolgozta ki végül a módszert, amely szerzőkhöz és szövegekhez n-dimenziós vektorokat rendel, s ezután elhelyezi őket az n-dimenziós térben, s ezen vektorok távolságát összehasonlítva igyekszik megválaszolni a végső kérdést: Ki a Nachtwachen szerzője?
Tekintettel arra, hogy témánk a matematika és a nyelvészet kapcsolata, így a válasz megadása előtt tegyünk egy kis kitérőt, és nézzük meg, mit jelent egy n-dimenziós vektortér! Korábban volt szó róla, hogy a matematika nyelve, és annak logikája sokszor teljesen másként működik, mint a hétköznapi beszélt nyelv. Így a tér fogalma A magyar nyelv értelmező szótára szerint is, főnévként elsődlegesen a filozófiai értelemben vett tér, „az anyag létezésének az a formája, amelyet a három irányú kiterjedés jellemez.” (Bárczi–Országh 1959–1962). Ez tulajdonképpen a mindenki által ismert 3-dimenziós tér, amely körülvesz minket. A matematikában azonban a tér egy általános fogalom, egy modell, amely különböző pontokból áll, s lehetnek alacsonyabb és magasabb dimenziósak is, egészen a végtelen dimenziós terekig. Ezek segítségével vizsgálhatók különböző folyamatok, jelenségek, így például adott esetben egy nyelvészeti kérdés is.
A dimenzió tulajdonképpen azt jelenti, hogy a térben hány lényegesen különböző irány, úgynevezett független vektor található, amely meghatározza az egész teret. Ezeket a vektorokat nevezzük a tér bázisának. 1 dimenzióban ez egyetlen egyenes iránya, ekkor bármely vektort választjuk ki, az megfelelő mennyiségekkel szorozva előállítja az összes többi vektort. Azaz adott bázisban minden pont egyértelműen megadható egy valós számmal, ezek távolsága a két szám különbsége. 1-dimenziós pontok köré is felvehető egy gömb, mely egy adott távolságon belül lévő pontok halmaza. Ezt láthatjuk a 2-es ábrán.

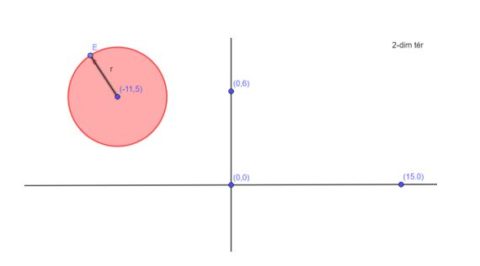
Magasabb dimenziók felé haladva növekszik a bázis elemszáma. 2 dimenzióban már két független irány található (3. ábra). Ez a szokásos Descartes-féle derékszögű koordinátarendszer, úgynevezett ortonormált bázissal, de természetesen rengetegféleképp megkonstruálható a 2-dimenziós tér. Ilyenkor minden pont meghatározásához két szám szükséges, a köré írt gömb pedig egy 2-dimenziós kör lesz.
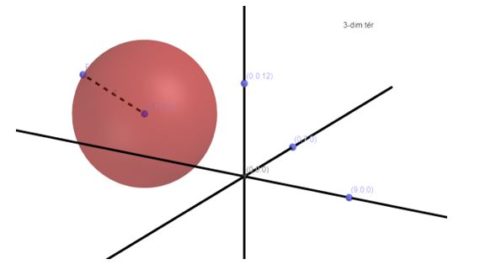
A 3-dimenziós tér a mindenki által jól ismert tér, a prototipikus gömbbel (4. ábra). A magasabb dimenziós tereket már nem tudjuk ábrázolni, csak elméletben megkonstruálni, s a matematika eszköztárával könnyen kezelhetővé tenni.
A Wickmann-módszer tehát abban áll, hogy meghatároz különböző grammatikai elemeket, szövegekben megfigyelhető, számokkal jellemezhető mennyiségeket, például mondathossz, szóhossz stb. Minél több változót használ, annál nagyobb valószínűséggel ad pontos eredményt a vizsgálat. Wickmann körülbelül 100 paramétert határozott meg a német nyelvre vonatkozóan. Így kapott egy 100-dimenziós vektorteret, melyben elhelyezhette a lehetséges szerzők pontjait, a stílusuk alapján meghatározott sugarú köréjük írt gömböket és a Nachtwachenhez rendelt pontot. A módszer nem vitt közelebb a szerző meghatározásához, mégis forradalmi eredményt mutatott fel: a négy lehetséges szerző közül nagyon nagy valószínűséggel egyik sem írta a kérdéses művet. De akkor ki a szerző? Majdnem két évtizeddel később, 1987-ben sikerült megállapítani, hogy a Nachtwachen szerzője August Klingemann, s ezt azóta levéltári adatokkal is bizonyítani tudták, így a rejtély végleg megoldódott. (Haag 1987: 81.)
További érdekesség a módszer kapcsán, hogy egyértelműen nyelvspecifikus, így a német nyelven kívül más nyelvekre értelemszerűen nem alkalmazható automatikusan. Azonban a disszertáció megjelenését követően Wickmannt felkereste az izraeli főrabbi, aki aziránt érdeklődött, hogy a bibliai Mózes öt könyvét írhatta-e egyetlen ember. Így a német matematikus Izraelbe költözött, megtanulta a héber nyelvet, majd tanulmányozta a Tórát, s átdolgozta a módszerét a héber nyelvre. Ezek után megállapította, hogy legalább három lényegesen különböző rész található a szövegekben, amiket biztosan nem írhatott egyetlen ember. Azonban azon túl, hogy ez a felfedezés óriási meglepetést kelthet, annak eldöntése, hogy Mózesnek tulajdonítható-e az öt könyv, sokkal inkább az egyház feladata marad.
A fenti példa tehát jól bizonyítja, hogy a nyelvészet, az irodalomtudomány vagy a filológia sokszor nem áll teljesen távol a matematikától, amely nem mellesleg sokáig bölcsészettudományként volt számon tartva. A matematika attól szép, hogy könnyen kezelhető, egzakt és egyértelmű, ezért olyan képlékeny területeken alkalmazva is segítséget nyújthat mint egy mű szerzőjének vizsgálata. Mindezek fényében azt reméljük, hogy jelen beszámolónkkal sikerült azok számára is felkeltenünk a matematika iránti érdeklődését, és eloszlatni a vele kapcsolatos félelmeit, akik eddig bölcsészként csak tisztességes távolból tekintettek efelé az ősi és csodaszép tudomány felé.
Szakirodalom:
Haag, Ruth 1987. Noch einmal. Der Verfasser der „Nachtwachen von Bonaventura”, 1804. Euphorion. 81.
Lauter, Josef 1966. Untersuchungen zur Sprache von Kants „Kritik der reinen Vernunft”. Westdeutscher Verlag. Köln und Opladen.
Wickmann, Dieter 1969. Eine Mathematisch-Statistische Methode zur Untersuchung der Verfasserfrage literarischer Texte. Durchgeführt am Beispiel der >>Nachtwachen. Von Bonaventura<< mit Hilfe der Wortartübergenge. Aachen.
Nincs hozzászólás!